Work Packages
JHPC-quantum

06.
Research and Development of Programming Environment for Quantum HPC Hybrid Platform
Accelerate development of quantum algorithm and application with HPC simulation
Overview
Quantum computers are currently suffering from their low reliability, which hinders the development of quantum algorithms and applications. The simulation of quantum computers on (classical) computers is a useful tool to alleviate this situation. In this project ⑥, we will focus on the development of quantum computer simulation on HPC. We will develop a simulator that uses the highly versatile state-vector method and a simulator that uses the tensor network method that can handle a large number of qubits.
Detail
Quantum computers are expected to be able to solve problems that are difficult or inefficient to handle with conventional (classical) computers. In recent years, as the technology for its realization has begun to mature, vigorous research and development has been underway. As of 2024, quantum computers that can freely perform gate processing on over 100 qubits have already been put into practical use, but malfunctions occur more than a few times per 1,000 times of gate operations, and the state of the qubits is maintained for at most a few thousand to tens of thousands of operations. Furthermore, since there are only a few dozen quantum computers in the world, the processing time available to users is limited, and long waiting times for processing are common. This also limits research and development activities for quantum algorithms and applications.
Under these current circumstances, quantum computer simulations using conventional (classical) computers are also being utilized for quantum computer research, development, and education. Simulation is supporting rapidly developing quantum information processing technology that compensates for the lack of computational resources of quantum computers, provides highly reliable simulation results without malfunction, and makes it easy to know the quantum state during quantum processing if necessary. It is a key technology that supports the smooth development of the quantum world.
In quantum computer simulation, the quantum mechanical states of a large number of qubits are expressed as (classical) numbers in a (classical) computer, and various transformations and transformations corresponding to processing on a quantum computer are applied to that representation. Perform simulations. N qubits are represented as a set of 2N complex numbers. The method of sequentially simulating the operation of a quantum computer using this kind of representation is called the "state vector method" and is the basic method of quantum computer simulation.
The state vector method is a method that can accurately simulate any kind of quantum processing, but it has the disadvantage that increasing the number of qubits requires storage capacity that explodes exponentially. When using double-precision complex numbers with over 16 significant digits in decimal notation, 16 bytes(B) of storage capacity is required for each complex number. In this case, a quantum computer with 10 qubits can be simulated with 16KiB, whereas 20 qubits would require 16MiB, and 30 would require 16GiB. This much information needs to be read and written for each quantum operation, and a personal computer or desktop workstation can handle up to 30 qubits. In quantum computer simulations, the computational processing required to convert and calculate the read and written information is small compared to the time required to read and write state information. In other words, the ability to transfer information for reading and writing determines the performance of the simulator. For this reason, simulating more qubits requires more storage capacity, and the ability to transfer information will determine the performance of the simulator. This is where HPC (High-Performance Computer), also known as supercomputers, comes into play. Current HPC maximizes the information transfer capacity of the entire system by connecting many computers through communication paths with high information transfer capacity. For example, "Fugaku" consists of 158,976 nodes connected by the TofuD network, and each node can transfer up to 40.8 GiB per second with other neighboring nodes. Each node has 32GiB of storage, 52 CPU cores (48 of which are available to users), and can read and write up to 1 TiB per second. Assuming that each node uses 16 GiB to represent the state of a qubit, 40 qubits can be simulated by using 1,024 nodes of the Fugaku. Such 1,024-nodes job is a small job in the Fugaku jobs, so you can run it at any time without stress.
The RIKEN Center for Computational Science has been researching and developing quantum computer simulation technology for many years in cooperation with supercomputer centers in various countries, and has developed a state vector simulator called "braket" for parallel computers that uses inter-node communication using MPI(This braket is different from the simulator of the same name recently developed by Amazon). As shown in Figure 1, which shows the performance when simulating using the Fugaku with the braket, one process can be simulated in about 1 second. For the red line using 16GiB per node, 1,024 nodes are used to simulate 40 qubits, and typically 32,768 nodes can be used to achieve up to 45 qubits, subject to the limit on the number of nodes available to the user. In the case of the green line, which uses 24 GiB per node, it uses 49,152 nodes and can handle up to 46 qubits. The above result is when double-precision complex numbers are used, but if you use single-precision complex numbers, you can handle one more qubit, half-precision allows two, and byte-precision allows you to handle three more qubits. Also, if you use the entire of the Fugaku, you will reach around 50 qubits. Figure 2 shows an example of material design using the quantum variational method using this braket.
With the state vector method, there is a limit to the number of qubits that can be simulated due to storage capacity limitations, but a method known as the “tensor network method'' is known as a method that overcomes this limit. The tensor network method is a method in which quantum computer processing is simulated by cutting it into blocks of processing for a small number of qubits, and then connecting the simulation results to simulate the original processing. Although it is not always possible to cut the pieces efficiently, there are examples of efficient cutting and stitching for some problems, and simulations of up to about 10,000 qubits are possible on HPC system. In this project item ⑥, we are also conducting research and development of the tensor network method.
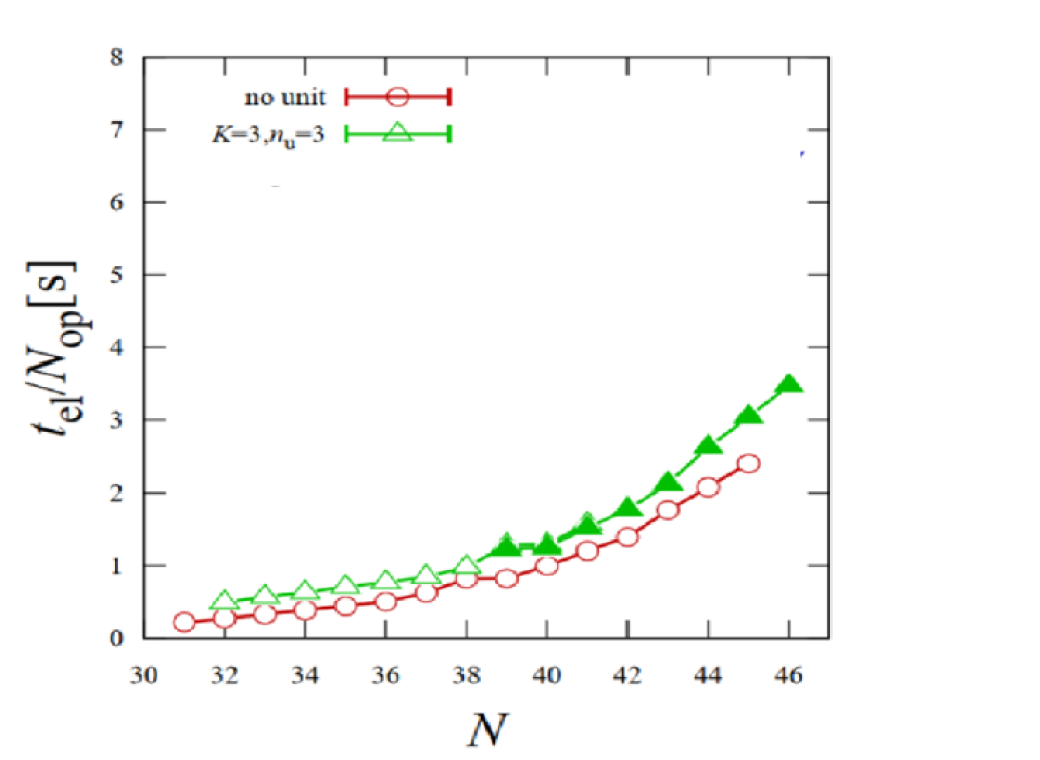
Figure 1: Time required to simulate one operation of a quantum computer with N qubits (horizontal axis) using the Fugaku with the braket (vertical axis). The average time required for processing per gate is plotted in seconds when Hadamard gates are sequentially applied to each qubit. The red line is when 16GiB is used per node, and the green line is when 24GiB is used. In the green case, compared to the red case, a simulation with the same number of qubits is realized with a smaller number of nodes, and although the processing time is slightly longer, the processing can be performed with fewer computational resources (execution time times number of nodes).
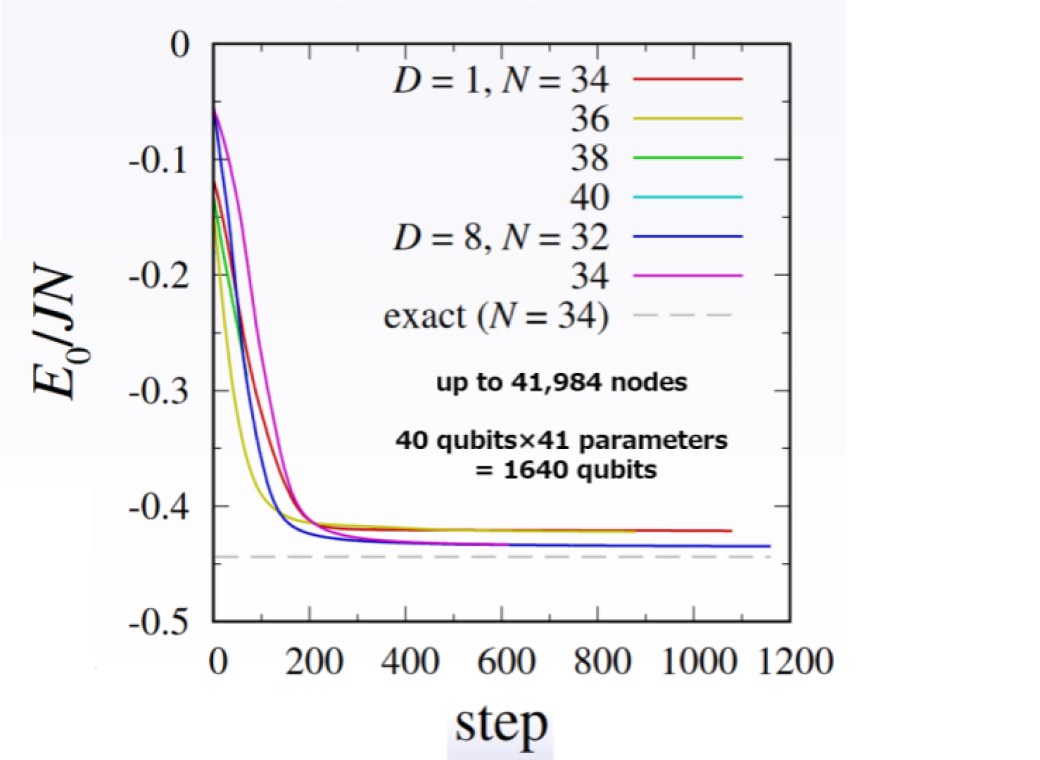
Figure 2: Shows the results of a quantum algorithm that evaluates the ground state energy of the quantum Heisenberg model using the quantum variational method, simulated by the Fugaku using the braket. This shows how a system consisting of N quantum Heisenberg spins is converged to near the ground state energy by repeating variational calculations. The case using the quantum mechanical variational state of D=1 and the case of D=8 are shown, but D=8 is closer to the correct value shown by the dashed line and is a better variational state. It turns out that it is. This simulation uses 41,984 nodes of the Fugaku from generation to generation, and is the result of a rigorous numerical simulation of 1,640 qubits.
Project Members
RIKEN Center for Computational Science
Project Leader
- Nobuyasu Ito
- Quantum-HPC Hybrid Platform Division Quantum Computing Simulation Unit
- Naoto Aoki
- Quantum-HPC Hybrid Platform Division Quantum Computing Simulation Unit
- Tomonori Shirakawa
- Quantum-HPC Hybrid Platform Division Quantum Computing Simulation Unit
- Naoki Yoshioka
- Quantum-HPC Hybrid Platform Division Quantum Computing Simulation Unit
- Sun Rongyang
- Computational Materials Science Research Team