Development and Assessment of Quantum-HPC Hybrid Applications

By using the quantum-supercomputer hybrid platform, we aim to achive computations that exceed the capability of classical computers

Overview

In this project, we will demonstrate the effectiveness of the quantum-supercomputer hybrid platform. To achieve this, we will develop quantum algorithms for quantum many-body systems in research fields such as condensed matter physics, quantum chemistry, and particle and nuclear physics, where the use of NISQ computers without error correction is expected to be beneficial. Furthermore, we will aim to realize quantum computations that exceed the limits of classical computation in at least one application using this platform.

Detail

To demonstrate the effectiveness of the quantum-supercomputer hybrid platform, we will implement the following six applications:

（1） Quantum dynamics
（2）Quantum thermodynamic calculations
（3）Optimization problems based on quantum variational methods
（4）Optimization problems beyond quantum variational methods
（5）Electronic state calculations based on quantum embedding methods
（6）Low-energy state calculations by a quantum-selected configuration interaction method

In these applications, the execution of computations that are beyond the scale of qubits manageable by state vector method simulations on classical computers, and that exceed the circuit depth achievable by approximate classical methods such as tensor network calculations, will serve as a benchmark for demonstrating the effectiveness of computations that surpass the limits of classical computation. The details of each application are explained below.

（1）Quantum dynamics

Quantum dynamics refers to the phenomenon of time evolution of quantum states, which correspond directly to quantum gate operations on a quantum computer. The time evolution of quantum states generally involves an increase in quantum entanglement, making long-time quantum dynamics difficult to simulate using classical computers based on tensor network methods. Therefore, quantum dynamics is one of the most promising applications for realizing quantum computations that surpass the limits of classical computation.
In this project, we will focus on quantum dynamics calculations based on quantum many-body Hamiltonians. To verify the effectiveness, advanced HPC and simulations using classical algorithms that leverage HPC will be essential. Therefore, this project will collaborate with Project item 6, conducting classical calculations using HPCs such as Fugaku. Additionally, certain classes of dynamics, such as Clifford circuits, can be simulated in polynomial time using classical computers, and these will also be used as benchmarks for quantum computation. If we can perform quantum dynamics calculations for two-dimensional quantum systems that exceed the computational capability of classical calculations, this could lead to new discoveries in fundamental research, deepen our understanding of phenomena such as quantum many-body localization and discrete time crystals, and help resolve related issues.
　Moreover, quantum circuits for quantum dynamics represent the most simplified form of quantum circuits used in general quantum computations. Therefore, the development of quantum computing techniques for quantum dynamics and the understanding of the principles of the quantum computation are important fundamental elements for implementing more complex quantum computations.

（2）Quantum thermodynamic calculations

In statistical mechanics, which describe the properties of quantum systems at finite temperatures, these states are usually represented as mixed states, but they can also be described as pure states. The description as pure states can be achieved through the purification of the density matrix or thermal pure quantum states.
In this project, considering the effective use of currently available quantum computers, we will focus on the development of quantum thermodynamic calculations based on thermal pure quantum states, using random quantum states or scrambled quantum states. As a statistical ensemble, we consider, for example, the microcanonical ensemble. The microcanonical ensemble is an ensemble of states with specified energies within a certain range. The physical quantities of this ensemble can be obtained as the Fourier transform of the time-evolved (quantum-dynamics) physical quantities, thereby leveraging the insights gained in i) Quantum Dynamics. However, multiple applications of controlled time evolution operator are required in the quantum circuit, making it a more challenging task than quantum dynamics (see Figure 1).

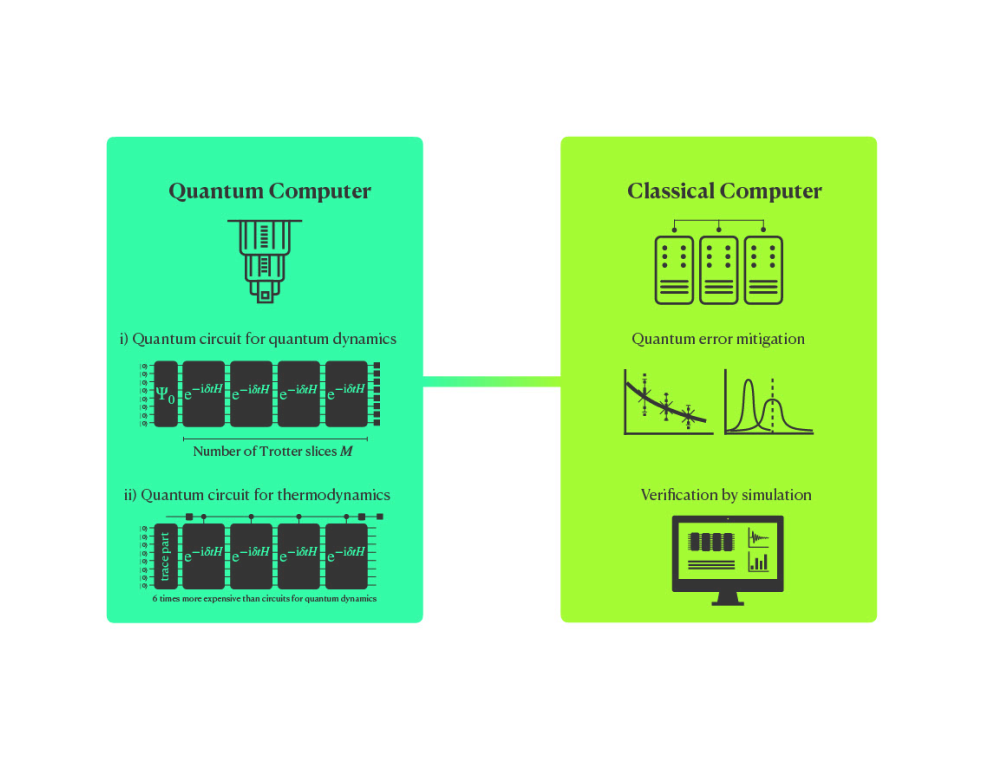
Fig. 1: Schematic diagrams for i) quantum dynamics and ii) quantum thermodynamics calculations

On the other hand, since only a single ancillary qubit needs to be measured, the readout error mitigation is expected to be easier than in quantum dynamics calculations. To perform general controlled time evolution operations, a quantum computer that allows quantum gate operations between any two qubits (for example, trapped-ion quantum computers) is more suitable.

（3）Optimization problems based on quantum variational methods

Various quantum-classical hybrid algorithms have been proposed to solve optimization problems by applying the rotation angles of qubit rotations as variational parameters in quantum circuits and introducing appropriate cost functions. Representative examples include the variational quantum eigensolver (VQE) for ground and excited states of quantum many-body systems and the quantum approximate optimization algorithm (QAOA) for combinatorial optimization problems. These methods have demonstrated effectiveness in small-scale computations, but further investigation is needed to determine whether they are scalable when the number of qubits increases. Additionally, it is necessary to clarify how to select the appropriate quantum circuit structure depending on the problem and to understand the dependency of the phenomenon where the gradient of the cost function becomes zero (known as the barren plateau) as the number of variational parameters increases, on the quantum circuit structure.
In this project, to solve and reduce these difficulties, we will develop methods to construct better quantum circuits for individual problems by analysis based on tensor decomposition methods, such as the tensor network method for quantum states by classical computation and tensor learning, a machine learning technique. These methods will be applied to ground state calculations of quantum many-body systems and combinatorial optimization problems. Furthermore, we aim to accelerate tensor contraction computations by using quantum computers with a large number of qubits, which will be installed in this project (see Figure 2).

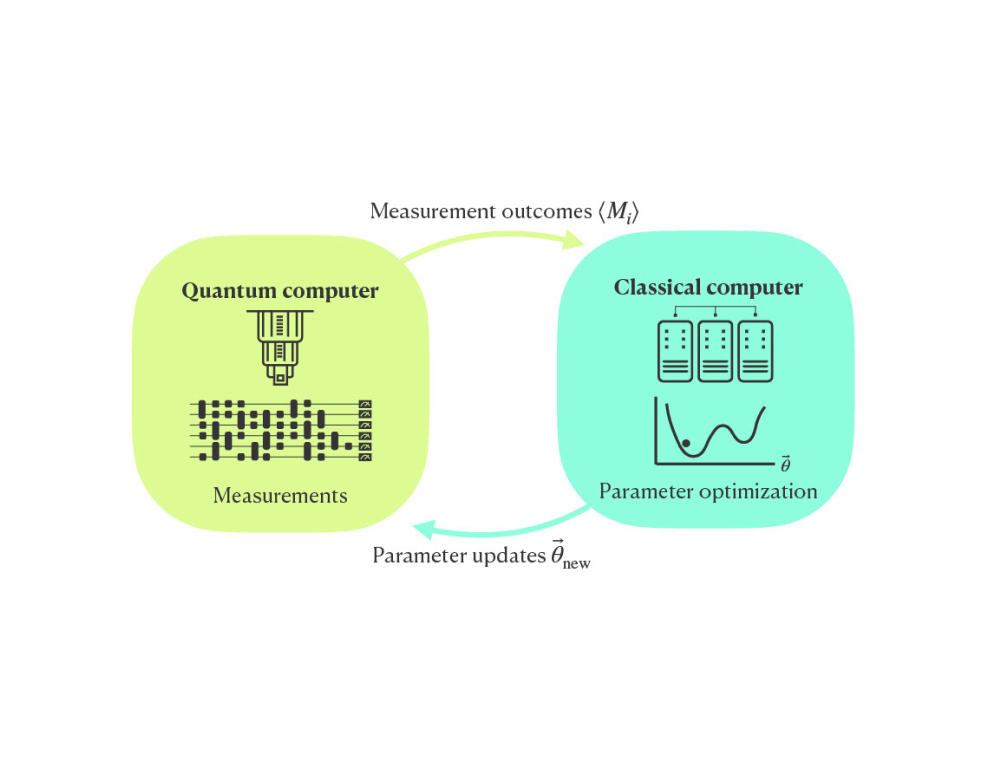
Figure 2: Schematic figure for iii) optimization problems based on quantum variational methods.

（4）Optimization problems beyond quantum variational methods

Quantum variational methods have been extensively studied and developed as a foundation for quantum-classical hybrid computation. However, these studies have revealed several issues to be overcome. On the other hand, to address these issues, quantum algorithms for optimization problems beyond quantum variational methods, which do not involve the optimization of variational parameters by classical computers, have been actively studied. In particular, methods classified as quantum-subspace techniques have the advantage of not requiring the optimization of variational parameters. However, there methods also present challenges, such as the need to generate a subspace that accurately represents the target states (e.g., ground state or excited states), and the selection of the subspaces often depends on physical considerations, prior knowledge, or empirical rules.
In this project, we will implement quantum subspace methods on the quantum-supercomputer hybrid platform, and perform calculations for ground states of quantum many-body systems and combinatorial optimization problems, to verify the effectiveness.

（5）Electronic state calculations based on quantum embedding methods

Transition metal oxides with various functionalities such as superconductivity, and metalloproteins containing transition metals that are crucial in processes like photosynthesis, belong to a class of materials known as strongly correlated materials or molecules, characterized by strong electron correlation. Understanding and predicting the properties based on their electronic states is an important issue in materials science. In classical calculations, methods such as the dynamical mean-field theory (DMFT) and multi-configuration self-consistent field (MCSCF) methods have achieved some success by dividing the real space or energy space into two regions, the complete active space and the other regions, where electron correlations are accurately treated in the active space and the interactions between these two regions are treated approximately (embedded methods). However, since the computational accuracy depends on the dimensionality of the complete active space, classical computers struggle with large-scale systems.
　In this project, we aim to develop a quantum embedding method that integrates quantum and classical computations, and demonstrate its effectiveness on strongly correlated models such as the Hubbard model. In this hybrid approach, the quantum computer will handle the electronic states in the complete active space, which would otherwise require exponentially increasing computational time with the number of orbitals in classical calculations. The remaining low-cost calculations will be performed on classical computers. We will develop and evaluate various methods, including VQE calculations based on the quantum variational principle for the electronic state calculations in the active space, quantum Monte Carlo methods assisted by quantum computations to reduce the negative sign problem of the single-particle Green's function in the active space, and methods for solving the Dyson equation required for handling Green’s functions on quantum computers.
Another important issue in this project is the development and application of highly accurate calculations for excited states in many-body electronic systems. Previously, quantum-classical hybrid methods, including VQE calculations, have focused mainly on the ground state calculations. However, understanding the properties of materials requires not only ground states but also a thorough understanding of low-energy excited states. Therefore, we aim to develop methodologies for accurately handling excited states within the complete active space. Using the developed methods, we will calculate Green's functions and spectral functions of strongly correlated models and materials. The target models include multi-orbital Hubbard models, multi-orbital Hubbard-Holstein models with phonon degrees of freedom, Anderson models, and Kondo lattice models, all of which are actively studied in the field of condensed matter physics.

（6）Low-energy state calculations by a quantum-selected configuration interaction method

In connection with(4) Quantum Algorithms for Optimization Problems beyond Quantum Variational Methods, we will develop quantum-classical hybrid algorithms for the selected configuration interaction method, a quantum-selected configuration interaction (QSCI) method, which systematically approaches the accuracy of the full-configuration interaction (FCI) method, the most accurate method in the field of quantum chemistry (see Fig. 3). Using this method, we will demonstrate the effectiveness on a many-body hydrogen atom model of a scale that is difficult for FCI calculations on existing classical computers. Furthermore, we will expand its application to other strongly correlated molecules, as well as to problems in condensed matter physics and particle and nuclear physics. Since the QSCI approach is an algorithm developed in collaboration with members of Osaka University, we will work closely with Project item 4

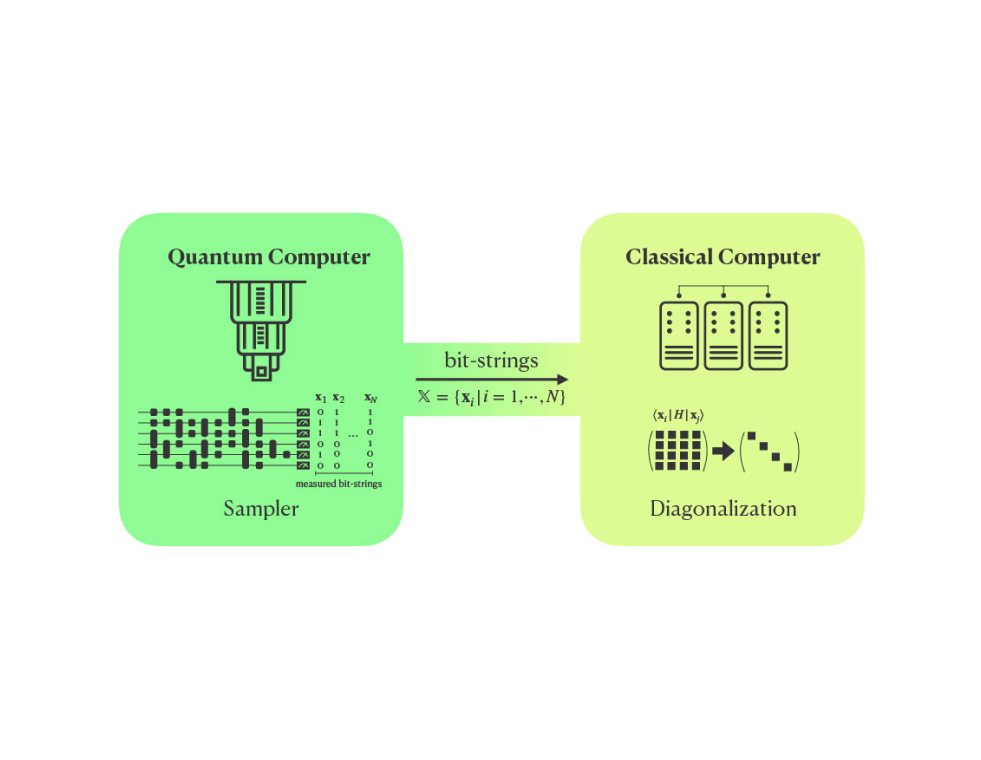
Figure 3: Schematic figure for a quantum-selected configuration interaction (QSCI) method .

Project Members

RIKEN

Project Leader

Seiji Yunoki: Center for Computational Science Computational Materials Science Research Team
Ryotaro Arita: Center for Emergent Matter Science Computational Quantum Matter Research Team
Tatsuhiko Ikeda: Center for Quantum Computing Quantum Computing Theory Research Team
Kenichi Ishikawa: TRIP Headquarters Trapped Ion Quantum Computer Team
Etsuko Ito: Interdisciplinary Theoretical and Mathematical Sciences Program
Erik Viktor Loetstedt: TRIP Headquarters Trapped Ion Quantum Computer Team
Yuichi Otsuka: Center for Computational Science Operations and Computer Technologies Division
Masanao Ozawa: Innovation Design Office
Dongwook Ghim: Interdisciplinary Theoretical and Mathematical Sciences Program
Hidehiko Koshiro: Center for Computational Science Computational Materials Science Research Team
Jishnu Goswami: Center for Computational Science Field Theory Research Team
Shiro Sakai: Center for Emergent Matter Science Computational Quantum Matter Research Team
Takeshi Sato: TRIP Headquarters Trapped Ion Quantum Computer Team
Kazuya Shinjo: Center for Emergent Matter Science Computational Quantum Matter Research Team
Tomonori Shirakawa: Computational Materials Science Research Team
Jun Seita: Information R&D and Strategy Headquarters Advanced Data Science Project Medical Data Deep Learning Team
Kazuhiro Seki: Center for Quantum Computing Quantum Computational Science Research Team
Shigetoshi Sota: Center for Computational Science Operations and Computer Technologies Division
Kazuma Nagao: Center for Computational Science Computational Materials Science Research Team
Maho Nakata: Cluster for Pioneering Research Computational Condensed Matter Physics Laboratory
Takanori Nishi: TRIP Headquarters Trapped Ion Quantum Computer Team
Steffen Backes: Interdisciplinary Theoretical and Mathematical Sciences Program
Tetsuo Hatsuda: Interdisciplinary Theoretical and Mathematical Sciences Program
Tomoya Hayata: Interdisciplinary Theoretical and Mathematical Sciences Program
Han Xu: Center for Computational Science Computational Materials Science Research Team
Juan Pedersen: Center for Quantum Computing Quantum Computational Science Research Team
Himadri Pathak: Interdisciplinary Theoretical and Mathematical Sciences Program
Shunji Matsuura: Interdisciplinary Theoretical and Mathematical Sciences Program
Yuta Murakami: Center for Emergent Matter Science Computational Quantum Matter Research Team
Kaoru Yamanouchi: TRIP Headquarters Trapped Ion Quantum Computer Team
Yasushi Yoneta: Center for Quantum Computing Quantum Computing Theory Research Team
Lukas Broers: Center for Computational Science Computational Materials Science Research Team
Sun Rongyang: Center for Computational Science Computational Materials Science Research Team

back to the list