量子・HPC連携アプリケーションの研究開発と有効性の実証

量子・スパコン連携プラットフォームを活用し、古典コンピュータの計算可能限界を超える計算の実現を目指します

概要overview

本課題では、本プロジェクトで構築される量子・スパコン連携プラットフォームの有効性を実証します。そのために、エラー耐性のないNISQコンピュータの活用が有用であると期待される物性物理学、量子化学、素粒子・原子核物理学などの分野において、量子多体系に対する量子アルゴリズムを開発します。また、このプラットフォームを用いて、古典計算の限界を超える量子計算を少なくとも一つのアプリケーションで実現します。

事業内容detail

量子・スパコン連携プラットフォームの有効性実証のため、以下の6つのアプリケーションを実施します。

（1）量子ダイナミックス
（2）量子熱力学計算
（3）量子変分法に基づく最適化問題
（4）量子変分法を超えた量子最適化問題
（5）量子埋め込み法に基づく電子状態計算
（6）量子選択配置間相互作用法による低エネルギー状態計算

これらのアプリケーションにおいて、古典コンピュータを用いた状態ベクトル法シミュレーションが扱えない規模であり、かつテンソルネットワーク計算などの近似手法で到達できない計算サイズを超える回路長のアプリケーションの実行が、古典計算の限界を超えた計算として有効性実証の目安となります。以下に各アプリケーションの詳細を説明します。

（1）量子ダイナミックス

量子ダイナミックスとは、量子状態の時間発展現象を指し、これは量子コンピュータ上での量子ゲート操作に他なりません。量子状態の時間発展は、一般にその量子状態を保持する量子ビット間の量子エンタングルメントの増大を伴うため、長時間の量子ダイナミックスはテンソルネットワーク法に基づく古典コンピュータでのシミュレーションが困難となります。したがって、量子ダイナミックスは古典計算の限界を超えた量子計算を実現するために最も有望なアプリケーションの一つです。

本課題では、量子多体系ハミルトニアンによる量子ダイナミックス計算を中心に行います。その有効性を検証するためには、最先端のHPCおよびHPCを活用した古典アルゴリズムによるシミュレーションが不可欠です。そのために、本課題では事業項目６と連携し、「富岳」をはじめとするHPCを用いた古典計算を実施します。また、クリフォード回路のような特定のクラスのダイナミックスは、古典コンピュータを用いて多項式時間でシミュレーションが可能であるため、これらも量子計算のベンチマークとして利用します。もし、2次元量子系に対する量子ダイナミックスを古典計算の可能領域を超えて計算できれば、2次元系における量子多体局在現象や離散時間結晶など、基礎研究における新たな発見、現象の理解の深化、および諸問題の解決につながります。

また、量子ダイナミックスの量子回路は、一般的な量子計算の量子回路の最も単純化した形態に相当します。したがって、量子コンピュータを用いた量子ダイナミックスに関する量子計算技術の開発および量子計算原理の理解は、より複雑な量子計算の実施に向けた基盤となる重要な要素です。

（2）量子熱力学計算

有限温度の量子系の性質を記述する統計力学では、その状態を混合状態として記述されることが多いですが、純粋状態として記述することも可能です。純粋状態としての記述には、密度行列の純粋化によるものと、熱的純粋状態によるものがあります。

　本課題では、現在利用できる量子コンピュータの有効利用を考慮し、ランダム状態または量子情報をスクランブルした状態を用いた熱的純粋状態に基づく量子熱力学計算の開発を中心に行います。統計集団として、例えばミクロカノニカル集団を考えます。ミクロカノニカル集団は、ある範囲内にあるエネルギーを特定した状態の集団ですが、このエネルギーを特定した状態の集団の物理量は、時間発展（量子ダイナミックス）させた物理量のフーリエ変換として得られるため、「(1)量子ダイナミックス」で得られた知見が活用されます。ただし、量子コンピュータで行う操作としては、制御時間発展が必要になるため、量子ダイナミックスよりも挑戦的な課題となります（図1参照）。

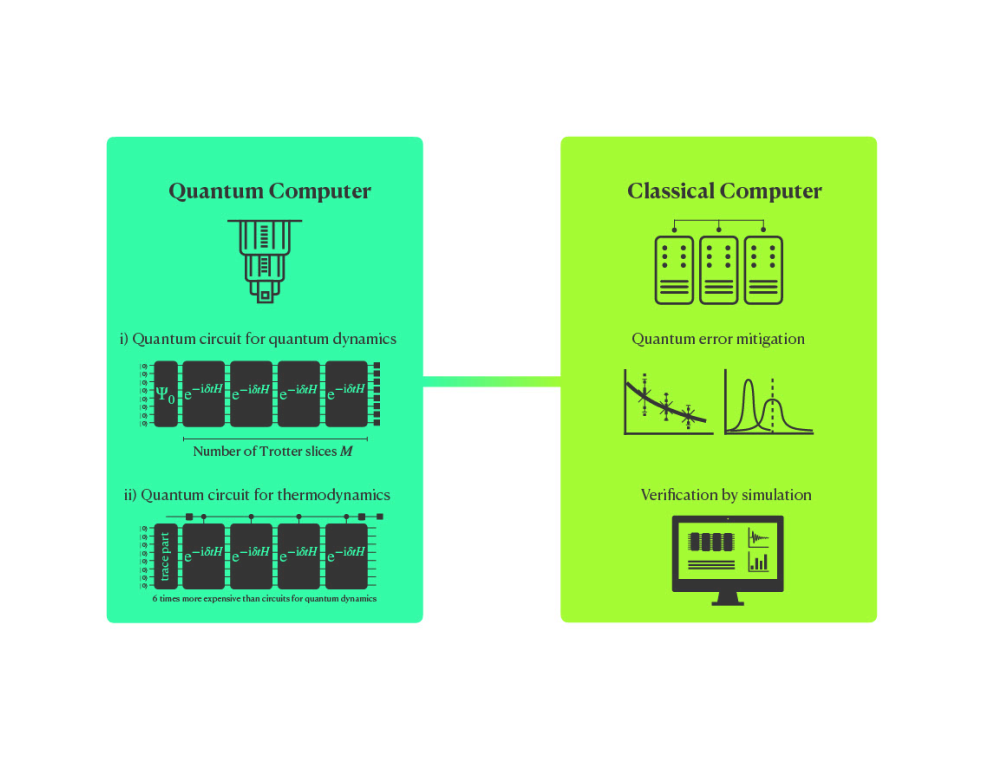
図1：(1)量子ダイナミックスおよび(2)量子熱力額計算に対する模式図

一方で、量子ビットの観測は１つの補助量子ビットの観測のみで済むため、観測時のエラーの取り扱いは量子ダイナミックス計算よりも容易になると期待されます。一般的な制御時間発展操作を行うには、任意の２つの量子ビット間で量子ゲート操作が可能な量子コンピュータ（例えば、イオントラップ型）が有効です。

（3）量子変分法に基づく最適化問題

量子ビット回転の回転角を変分パラメータとして量子回路に適用し、適切なコスト関数を導入することで、最適化問題を解く様々な量子-古典ハイブリッドアルゴリズムが提案されています。代表的な例としては、量子多体系の基底状態や励起状態に対する変分量子固有値法（VQE: Variational Quantum Eigensolver）や、組合せ最適化問題に対する量子近似最適化アルゴリズム(QAOA: Quantum Approximate Optimization Algorithm)などがあります。これらの方法は、小規模の計算においてはその実効性が示されていますが、量子ビット数を大きくした場合にスケーラブルな方法であるかどうかについては、さらなる検討が必要です。また、問題に応じてどのような量子回路構造を選択すべきか、変分パラメータ数が増加した場合にコスト関数の勾配がゼロになる現象が頻繁に発生しますが、これが量子回路の構造にどのように依存するかを明らかにする必要があります。

本課題では、これらの困難を解決・低減するために、古典計算による量子状態解析に対するテンソルネットワーク法や機械学習技法の一つであるテンソル学習などのテンソル分解法に基づく手法を活用し、個々の問題に最適な量子回路構造を構築する方法を開発します。この方法を量子多体系の基底状態計算や組み合わせ最適化問題などに応用します。さらに、本プロジェクトで導入される大規模量子ビットを持つ量子コンピュータを活用し、テンソル縮約の高速計算などを目指します（図2）。

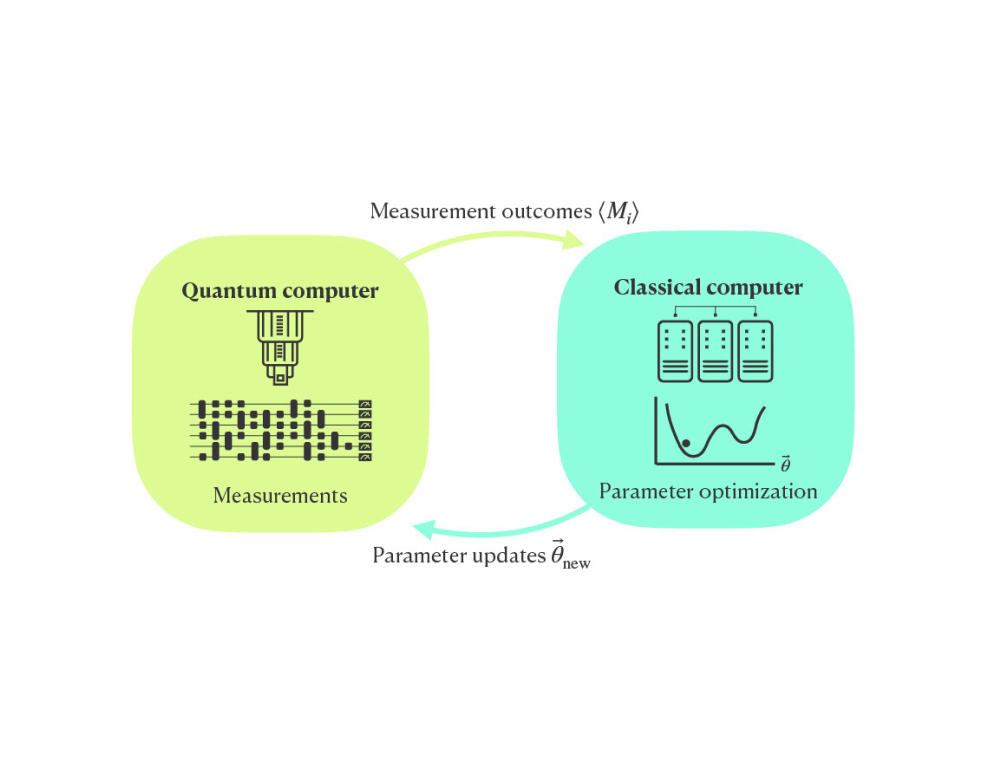
図2：(3)量子変分法に基づく最適化問題に対するする模式図

（4）量子変分法を超えた最適化問題に対する量子アルゴリズム

量子変分法は、量子-古典ハイブリッド計算の源流として世界中で研究開発が進められてきましたが、その結果、いくつもの課題が浮き彫りになってきました。一方で、これらの問題を回避するために、古典コンピュータによる変分パラメータの最適化を含まない、量子変分法を超えた最適化問題に対する量子アルゴリズムが盛んに研究されています。特に、量子部分空間法に分類される手法は、変分パラメータの最適化が不要であるという利点があります。ただし、狙った状態（例えば基底状態や励起状態）を良く表現できる部分空間を生成する必要があり、部分空間の選び方は物理的な考察や事前知識、経験則に基づく必要があるなど、課題も存在します。

本課題では、量子部分空間法を量子・スパコン連携プラットフォームに実装し、量子多体系の基底状態や組合せ最適化問題などの計算を実施し、その有効性を検証します。

（5）量子埋め込み法に基づく電子状態計算

超伝導など様々な機能を有する遷移金属酸化物や、光合成などで重要な遷移金属を含む金属タンパク質などは、電子間相関が強い物質群、つまり強相関物質・分子です。その電子状態に基づく物性の解明および予言は、物質科学において重要な課題です。古典計算による解析では、動的平均場近似や多配置自己無頓着場法などの方法で、実空間やエネルギー空間を電子間相関を正確に扱う領域（完全活性空間）とそれ以外の領域に分け、それらの間の相互作用を近似的扱う埋め込み法が一定の成功を収めています。しかし、計算精度は完全活性空間の次元に依存しており、古典コンピュータでは大規模な系に対しては困難が伴います。

本課題では、量子計算と古典計算をハイブリッドした量子埋め込み法を開発し、ハバード模型などの電子相関模型に対して実証します。古典計算では軌道数に関して指数関数的に計算時間が必要な完全活性空間の電子状態を量子コンピュータで計算し、それ以外の低コストな計算は古典コンピュータで行います。活性空間の電子状態計算法として、量子変分原理に基づくVQE計算や、電子状態を特徴付ける活性空間上のグリーン関数の負符号問題を低減する量子計算を援用した量子モンテカルロ法による計算、あるいはグリーン関数を扱う上で必要なダイソン方程式を量子コンピュータで解く方法などを開発し、その性能を評価します。

本課題におけるもう一つの重要なテーマは、多体電子系の励起状態を高精度に計算する方法の開発と応用です。従来、VQE計算をはじめとする量子-古典ハイブリッド技術は多体電子系の基底状態の計算に特化したものが中心でしたが、実際の物質の性質を理解するためには、基底状態だけでなく励起状態も重要です。そこで、完全活性空間について励起状態を正確に取り扱う方法論の開発を目指します。開発した方法を用いて、強相関模型や強相関物質のグリーン関数やスペクトル関数などの計算を行います。対象として、多軌道ハバード模型、フォノンの自由度を考慮した多軌道ハバードホルシュタイン模型、アンダーソン模型や近藤格子模型など、物性物理学の分野で活発に研究されているものが含まれます。

（6）量子選択配置間相互作用法による低エネルギー状態計算

「(4)量子変分法を超えた最適化問題に対する量子アルゴリズム」と関連して、量子化学分野で最も精度の高い全配置間相互作用法に系統的に精度を近づけることが可能な選択的配置間相互作用法の量子・古典ハイブリッドアルゴリズム（QSCI）の開発を行います（図3）。この手法を用いて、既存の古典コンピュータでは全配置間相互作用計算が困難な規模の水素原子模型に対して、その有効性を検証します。さらに、他の強相関分子系や物性物理、素粒子・原子核物理に関する問題にも応用を広げます。QSCIは大阪大学のメンバーも参画して開発されたアルゴリズムであるため、事業項目4と連携して研究開発を進めます。

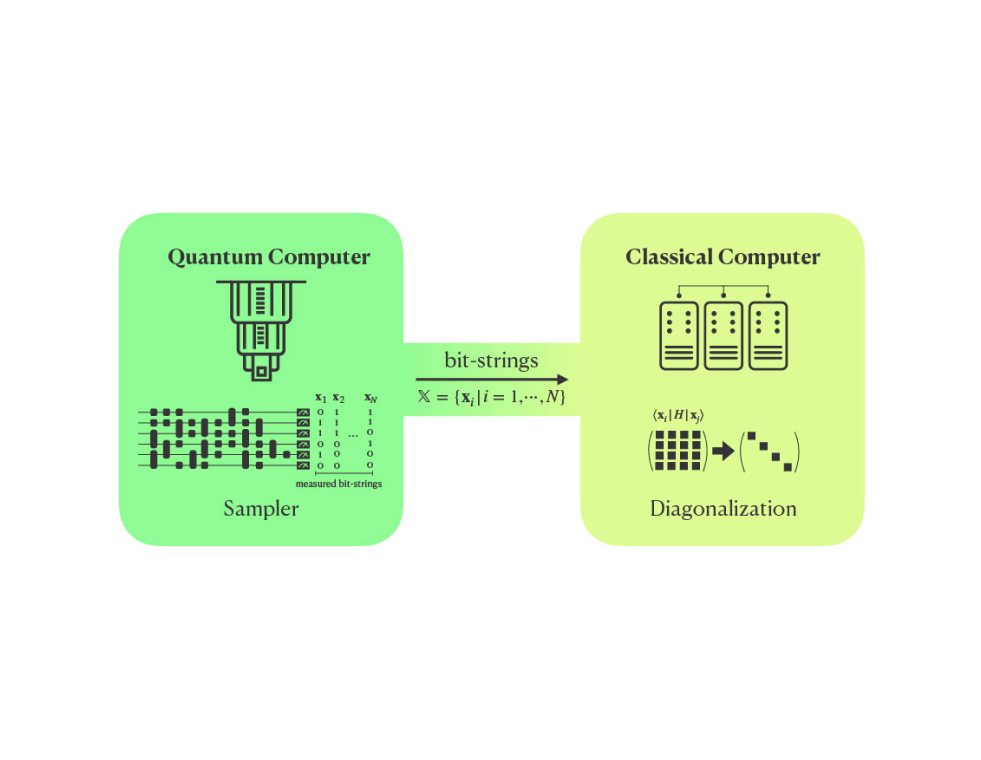
図3：(4)量子選択配置間相互作用法の模式図。

プロジェクトメンバーproject members

理化学研究所

プロジェクトリーダー

柚木清司: 計算科学研究センター量子系物質科学研究チーム
有田亮太郎: 創発物性科学研究センター計算物質科学研究チーム
池田達彦: 量子コンピュータ研究センター量子計算理論研究チーム
石川顕一: 最先端研究プラットフォーム連携(TRIP)事業本部イオントラップ量子計算機チーム
伊藤悦子: 数理創造プログラム
Erik Viktor Loetstedt: 最先端研究プラットフォーム連携(TRIP)事業本部イオントラップ量子計算機チーム
大塚雄一: 計算科学研究センター運用技術部門
小澤正直: 未来戦略室
Dongwook Ghim: 数理創造プログラム
幸城秀彦: 計算科学研究センター量子系物質科学研究チーム
Jishnu Goswami: 計算科学研究センター連続系場の理論研究チーム
酒井志朗: 創発物性科学研究センター計算物質科学研究チーム
佐藤健: 最先端研究プラットフォーム連携(TRIP)事業本部イオントラップ量子計算機チーム
新城一矢: 創発物性科学研究センター計算量子物性研究チーム
白川知功: 計算科学研究センター量子系物質科学研究チーム
清田純: 情報統合本部先端データサイエンスプロジェクト医療データ深層学習チーム
関和弘: 量子コンピュータ研究センター量子計算科学研究チーム
曽田繁利: 計算科学研究センター運用技術部門
長尾一馬: 計算科学研究センター量子系物質科学研究チーム
中田真秀: 開拓研究本部柚木計算物性物理研究室
西孝哲: 最先端研究プラットフォーム連携(TRIP)事業本部イオントラップ量子計算機チーム
Steffen Backes: 数理創造プログラム
初田哲男: 数理創造プログラム
早田智也: 数理創造プログラム
Han Xu: 計算科学研究センター量子系物質科学研究チーム
ピーダーセン珠杏: 量子コンピュータ研究センター量子計算科学研究チーム
Himadri Pathak: 数理創造プログラム
松浦俊司: 数理創造プログラム
村上雄太: 創発物性科学研究センター計算物質科学研究チーム
山内薫: 最先端研究プラットフォーム連携(TRIP)事業本部イオントラップ量子計算機チーム
米田靖史: 量子コンピュータ研究センター量子計算理論研究チーム
Lukas Broers: 計算科学研究センター量子系物質科学研究チーム
Rongyang Sun: 計算科学研究センター量子系物質科学研究チーム

一覧へ戻る